유로피안 옵션의 경우에 변동성이 높으면 값이 더 비싸다. ELS의 상품의 경우에는 그 반대이다. 왜냐하면 ELS는 구조적으로 풋옵션 매도 포지션이기 때문이다.
또한, 델타헷징을 통해 파생상품을 복제(replicate)하는 경우에도 헷징을 통해 얻게 되는 수익/손익과 변동성 값은 깊은 관계가 있다. 트레이더가 파생상품을 꾸준히 델타헷징을 하였다고 할 때 얻게되는 수익/손익은 역사적변동성(historical volatility)과 내재변동성(implied volatility)의 차이로 실현된다. 다르게 표현하면 30%의 내재변동성을 가정하고 발행한 파생상품을 트레이더가 헷지하여 복제하였을 때, 실제 역사적 변동성이 40%라면 변동성 제곱의 차이만큼을 추가로 벌게 된다.
즉, 대다수의 옵션은 주가와 시간을 입력변수로 갖는 비선형 함수로 표현할 수 있다. 그러면 이 함수를 주가의 polynomial 함수로 근사시킬 수 있다. 어떻게? 테일러 시리즈로 전개하면 된다. 이 때, 일차미분 텀을 텔타라 하고 - 이차미분 텀은 감마인데, 델타헤징이기 때문에 우선 무시해 두자 - 주가 변화량을 델타만큼 사고파는 것을 델타헤징이라고 한다. 이 과정을 옵션 발행부터 만기까지 하면 옵션을 구입한 것과 같은 효과를 기초자산을 매매하면서 만들어 낼 수 있다. 물론 이차미분 텀을 고려하지 않기 때문에 오차가 꽤 클 수 있다.
상품구조
ELS 상품은 다양한 구조를 가지고 있으며 이론적으로 무한개의 구조를 가질 수 있다. 주가 변화과정에 따라 수익이 결정되는 구조이니 너무도 명백하다. 여러 발행된 상품중에서 가장 큰 인기를 끌고 있는 상품은 기초자산 하나 혹은 두 개를 기반으로 한 스텝다운(Step-Down) 이다.
어떻게 수익을 만들어 낼까?
대부분의 사람들이 궁금해 하는 것은 '증권사는 어떻게 수익을 만들어 고객한테 돌려줄까?' 가 아닐까 싶다. 나도 ELS를 처음 접할 때 가장 궁금했었다. 간단히 설명하면 기본적으로 수익을 내기 위해서 기초자산으로 구성된 펀드를 운영한다고 보면 된다.
특징이라면 그 펀드를 운영하는 수학적인 룰을 상품의 구조가 정해지면 만들어낼 수 있다. 단지 기초자산의 단기/장기 전망이 좋을 것 같아서 혹은 PER, PBR이 높거나 낮아서 매매하는 것이 아니라 주가의 위치에 따라서 룰에 의해 매매여부와 수량이 결정된다. 이 룰을 계산해 내기 위해서는 수학과 컴퓨터를 다뤄야 하기 때문에 - 소위 말하는 금융공학 - 증권사에서 공대생들을 필요로 한다.

(c) yes24.com
ELW는 기본적으로 그 구조가 옵션과 동일하다. 콜ELW(풋ELW)의 경우 기초자산 가격이 만기일에 행사가격보다 높으면(낮으면) 가격차이 만큼 수익을 얻는 점에서 옵션과 동일하다. 옵션과 다른 점이라면 short sale이 안 되고, LP(liquity provider a.k.a. market maket) 에 의해 시장이 구성된다는 점이다.
ELW 투자를 목적으로 한다면 읽어봐야 할 책이다. 특히 ELW는 레버리지 효과를 일으키기 때문에 위험관리가 우선되어야 하는 투자수단이다. 거기에 좀 더 깊이 있는 지식을 원한다면, 그리고 미분방정식을 다룰 줄 아는 사람이라면 Black-Scholes 옵션가격결정모형에 대해 읽어보기를 권하고 싶다. 그래야 어떻게 가격이 결정되고 어떻게 움직일 것인지에 대해 예측이 가능할 것이기 때문이다.
이를 간단히 Matlab으로 표현하면 다음과 같다
mu = 0.1; % 주가 수익율
vol = 0.4; % 주가 변동성
dt = 0.01; % 시간 간격
for j = 1:100 % 100번 시물레이션
s(1, j) = 100; % 초기 주가는 100에서 시작
for i = 1:1000 % t0 에서 t1000까지 주가의 변화를 보았다
dz = randn * sqrt(dt); % brownian motion이 quadratic variation을 갖도록 함
ds = mu * s(i, j) * dt + vol * s(i, j) * dz; % GBM 주가 프로세스
s(i + 1, j) = s(i, j) + ds; % 새로운 주가
end
end
시물레이션 결과를 그래프로 확인하면 주가 변화는 다음과 같다.
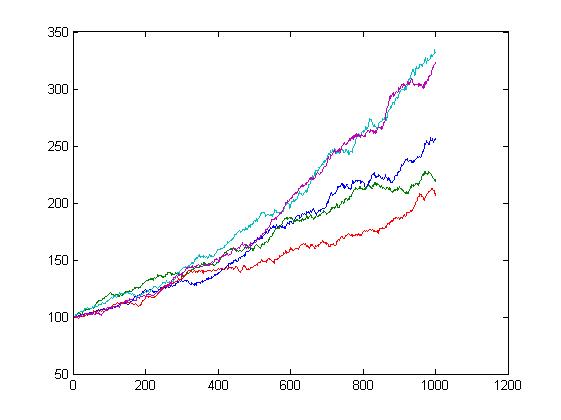
GBM에 의한 주가변화 모습
다음으로 Heston 주가 프로세스를 살펴보면 GBM과 두 가지 점에서 다르다. 하나는 변동성이 상수가 아니라 확률적인 과정(stochastic process)을 가진다는 것이고, 또 다른 하나는 변동성과 주가의 공분산이 음수라는 사실이다. 즉, 변동성의 방향과 주가의 방향이 반대라는 것을 의미한다. 이 두 가지 점에서 Heston 주가 프로세스는 좀 더 현실을 잘 반영한다.
이를 Matlab 코드를 나타내면 다음과 같다.
clear;
mu = 0.1; % 주가 기대수익율
dt = 0.01; % 시간간격
rho = -0.2; % 주가 확률과정과 변동성 확률과정 사이의 관계
LU = [1 0; rho sqrt(1-rho^2)];
k = 0.3; % kappa
sigma = 0.3; % 변동성 확률과정의 변동성
for j = 1:10
s(1, j) = 100; % 주가는 100에서 시작
v(1, j) = 0.5; % 변동성은 0.5에서 시작
for i = 1:1000
dw = LU * [randn; randn] * sqrt(dt); % 주가와 변동성 두 가지의 확률과정을 나타내었다.
ds = mu * s(i, j) * dt + sqrt(v(i, j)) * s(i, j) * dw(1, 1); % 주가 프로세스
dv = k * (mean(v(:, j)) - v(i, j)) * dt
+ sigma * sqrt(v(i, j)) * dw(2, 1); % 변동성 프로세스
s(i + 1, j) = s(i, j) + ds;
v(i + 1, j) = v(i, j) + dv;
end
end
시뮬레이션 결과를 그래프로 확인하면 다음과 같다.
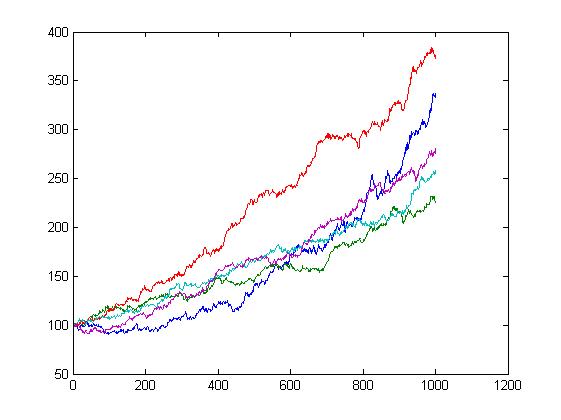
(c) sundayschoolcourse
콜옵션(call option), 풋옵션(put option)과 같이 옵션은 위험 자산이다. 은행이자처럼 확정된 값을 받는 것이 아니라 주식처럼 미래의 가치가 확정되지 않은 위험을 가진 자산이다. 하지만 미래의 값을 예측할 수 없는 주식과는 달리 조금 더 체계적인 위험을 가지고 있다. 옵션의 가격에 영향을 미치는 네 가지의 대표적인 위험요인에 대해 알아본다. 이 네 가지는 그리스 문자로 되어 있어 Greeks 이라고 표현한다.
델타(delta)
델타란 기초자산 – 일반적으로 주식 – 의 값이 변할 때, 파생상품의 가격이 변하는 정도를 나타낸다. 콜옵션의 델타 값이 0.2이면 주식의 값이 $1 오를 때, 콜옵션의 가격은 $0.2 오른다는 것을 뜻한다. 이를 이용하여 위험을 헷징하는 방법도 있다.
델타는 만기가 가까워오고 at-the-money 상황(옵션의 실행가격이 주가와 같을 때)에 있을 때, 증가하는 경향이 있으며 기초자산의 수준에 따라 값이 바뀐다. 또한 내재 변동성(implied volatility)의 변화에 의해서도 변한다. 만기가 가까울 때, 옵션가격은 좀 더 명확히 측정이 가능하기 때문에 at-the-money 상황에서는 주가의 증가 폭만큼 옵션의 가격이 상승하게 된다. 예를 들어 콜옵션 만기 하루 전에 주가가 $99이고 실행가격이 $99달러라고 하자. 가격이 그 다음날까지 그대로 유지된다면 옵션을 long(구입)한 사람은 $0를 벌며 옵션가격도 $0에 가깝게 된다. 만기일에 at-the-money 에서 장중 주가의 변화가 일어난다면 주가가 오른 만큼 옵션 가격도 상승한다. 델타 값은 1에 가까운 상황이기 때문에 주가가 장중 $100이 되었다면 옵션가격은 $1가 될 수 있을 것이다.
감마(gamma)
감마는 델타의 변화율을 측정하는 개념이다. 콜옵션이 out-of-the-money(현재주가가 실행가격보다 낮을 때)인 경우에는 낮은 델타 값을 가지고 델타의 변화율인 감마도 낮은 값을 가진다. 하지만 손익이 없는 at-the-money 상황에 가까워질수록 델타의 값은 커져가며 감마 값도 증가한다. 반대로 돈을 벌게 되는 상황인 in-the-money 상황이 커질수록 감마 값은 감소한다.
쎄타(theta)
옵션가격에는 두 가지의 가치가 포함되어 있다. 하나가 기초자산에 근거한 옵션의 내재가치(intrinsic value)라 한다면 나머지는 바로 시간가치이다. 즉, 옵션의 만기가 가까워올수록 시간에 의한 가치가 감소하게 되는데, 쎄타가 이를 반영한다.
옵션의 내재변동성이 매우 클 때, out-of-the-money 상황에서 쎄타 값은 매우 클 수 있으며 일반적으로 at-the-money 상황에서 가장 높다. 또한 쎄타 값은 거래 마지막 몇 주 동안 크게 증가하여 옵션을 long 한 사람들이 손실을 입을 수 있으며 내재변동성이 감소하는 상황에서는 더욱 그러하다.
베가(vega)
베가는 기초자산의 변동성에 따른 위험노출 정도를 측정하는 개념이다. 즉, 내재변동성의 변화에 따른 옵션가격의 변화로 정의된다. 예를 들면 베가가 높다는 것은 주가가 1시점에서 1만큼 변동하고, 2시점에서는 2만큼 변동하여 변동성이 1만큼 커졌을 때, 옵션의 가격변화가 크다는 것을 의미한다.
기초자산의 변동성만을 보기 때문에, 베가는 기초자산의 가격변화 없이도 증가하거나 감소할 수 있다. 만기가 가까울수록 감소하는 경향도 가지고 있다.
수식으로 나타내어지는 개념을 설명하라고 할 때, 수식을 풀어 말하는 사람은 창의력이 부족한 사람이다.알리안츠글로벌인베스터즈 이원일 대표
옵션(option)이란?
옵션은 만기일(maturity date)에 특정 자산(예: 주식, 이자율 등)을 특정 가격(exercise price)에 사거나 팔 수 있는 계약이자 권리이다. 그렇기 때문에 만기일에 특정 가격보다 자산의 가격이 높아지면 그 차익에서 옵션가격을 뺀 만큼의 이득을 볼 수 있다. 옵션은 공짜가 아니다. 반대로 자산의 가격이 특정 가격보다 낮으면 권리를 행사하지 않고 포기하기 때문에 옵션가격만큼의 손해를 보게 된다. 콜옵션(call option)은 자산을 살 수 있는 권리이고, 풋옵션(put option)은 팔 수 있는 권리이다. 따라서 풋옵션은 콜옵션과 반대로 자산가격이 특정가격보다 떨어져야 이익을 볼 수 있다.
옵션은 자산의 위험(risk)을 방어하기 위한 수단으로 사용된다. 주식을 하나 사고, 그 주식에 대한 콜옵션을 판다고 가정하자. 현재시점에서 콜옵션 가격만큼을 번다. 만기일에 주가가 오르면 콜옵션을 구입한 사람이 옵션을 행사하기 때문에 판매자에게 손해가 발생한다. 하지만 주식으로 돈을 벌게 되므로 이로 손실을 메꾼다. 반대로 주가가 떨어지면 주식은 손해이지만 콜옵션은 행사되지 않기 때문에 옵션을 판매하여 얻은 수익으로 주식으로 인한 손실을 메꾼다. 이렇게 위험을 방어할 수 있다.
블랙-숄즈 옵션 프라이싱 모델
옵션가격은 시장원칙에 의해 결정된다. 사려는 사람이 많으면 가격이 오르고 파려는 사람이 많으면 가격이 내린다. 옵션시장이 생긴지는 오래되었지만 블랙-숄즈 이전까지는 옵션의 가격을 결정하는 모델이 없었다.
블랙-숄즈가 옵션가격을 결정하는 방식은 위의 옵션으로 위험을 방어하는 예와 동일하다. 주식과 옵션으로 구성된 포트폴리오가 무위험 수익율을 내도록 방정식을 만드는 것이 옵션가격을 결정하는 핵심 아이디어이다. 즉, 옵션과 주식의 포트폴리오로 인한 차익거래가 불가능하도록 한다. 아이디어는 이렇지만 이를 실제로 구하려면 주가가 어떻게 움직이는가에 대한 (좀 어이없는)가정이 필요하며, 결론적으로 편미분 방정식을 풀어야 한다.
옵션의 델타(delta)
옵션의 델타란 기초자산 - 일반적으로 주식 - 의 가격변화에 대한 옵션의 가격변화의 비율을 말한다. 만약 옵션의 델타 값이 0.5라 하면 기초자산의 가격변화에 대해 옵션가격이 그 절반만큼 변한다는 것을 뜻한다. 주가가 $1 오르면 옵션은 $0.5 오른다. 이를 이용하여 헷징을 할 수 있다. 델타가 0.4일 때, 100개의 콜옵션을 팔고 0.4 * 100 = 40개의 주식을 산다고 가정하자. 이 경우 주식이 $1 올랐을 때, 옵션가격은 $0.4 오르고 0.4 * 100 = $40 의 손해를 본다. 하지만 이 때 1 * 40 = $40 의 이익을 주식으로 벌어 만회한다. 반대의 경우도 마찬가지다.
이를 확장하여 모든 자산의 델타값을 정의할 수 있다. 즉, 기초자산의 가격변화에 대한 파생상품의 가격변화가 된다. 이 때, 주식의 델타값은 1이다. 또한, 포트폴리오의 델타도 구할 수 있다. 포트폴리오의 델타는 각각 자산의 델타값과 그 수를 곱한 것을 모두 합하면 된다. 전체 포트폴리오의 델타값을 0으로 만드는 것을 델타헷징(Delta hedging)이라고 한다.



